[ALGORITHM] 3. 시간 복잡도(Time Complexity), Big-O notation

✅  시간 복잡도

입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것이다. 알고리즘의 시간복잡도는 주로 Big-O notation을 사용하여 나타내며, 이 Big-O notation은 계수와 낮은 차수의 항을 제외시키는 방법이다. 이런 방식으로 표현할 때, 시간복잡도를 점근적으로 묘사한다고 말한다.

 

 

✅  Big-O notation 

➰ O(1)

O(1)는 constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다. 입력값의 크기와 관계없이, 즉시 출력값을 얻어낼 수 있다는 의미이다. 코드 예시는 다음과 같다.

def print_first(arr):
    print(arr[0])

 

 

➰ O(n)

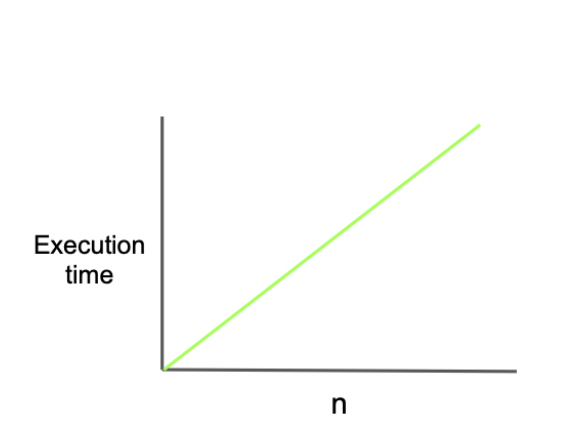
O(n)은 linear complexity라고 부르며, 입력값에 따라 시간 또한 비례해서 증가하는 것을 의미한다. 코드 예시는 다음과 같다.

def print_all(arr):
    for n in arr:
        print(n)

 

 

➰ O(log n)

O(log n)은 logarithmic complexity라고 부르며 Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다. 코드 예시는 다음과 같다. 이진 탐색 알고리즘이 대표적이다.

lower = 0
upper = len(numbers) - 1 
idx = -1
while (lower <= upper):
    middle = int((lower + upper) // 2)
    if numbers[middle] == target :
        idx = middle
        break
    elif numbers[middle] < target :
        lower = middle + 1
	else:
        upper = middle - 1

 

 

➰ O(n^2)

O(n^2)은 quadratic complexity라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다. 코드 예시는 다음과 같다.

def print_twice(arr):
    for n in arr:
        for x in arr:
            print(x, n)

 

 

➰ O(2^n)

O(2^n)은 exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가진다. 2^n만큼 증가한다는 것은 입력값(n)이 커질때 마다 시간이 2배로 늘어난다는 것을 의미한다. 코드 예시는 다음과 같다. 재귀로 구현한 피보나치 수열이 대표적이다.

def fibo(n):
    if n <= 1:
    	return n
    return fibo(n-1) + fibo(n-2)

 

 

➰ 성능 순서 : O(1) ➡️ O(log n) ➡️ O(n) ➡️ O(n^2) ➡️ O(2^n)